拓扑优化（Topology Optimization）浅谈

（近期刚刚完成了某产品吊重梁的拓扑优化分析，稍微整理下这方面的内容，如有不恰当的地方，还望各位大佬指正。）

拓扑优化（topology optimization）是一种根据给定的负载情况、约束条件和性能指标，在给定的设计区域内对材料分布进行优化的数学方法，是结构优化的一种。

结构优化可分为尺寸优化、形状优化、形貌优化和拓扑优化。

尺寸优化（Sizing design）：设计变量可能是杆的横截面积、板的厚度或是复合材料的分层厚度。

形状优化（Shape optimization）：以结构件外形或者孔洞形状为优化对象，比如凸台过渡倒角的形状等。

形貌优化（Topography optimization）：可以用来设计薄壁结构的强化压痕，以满足强度、频率等要求。

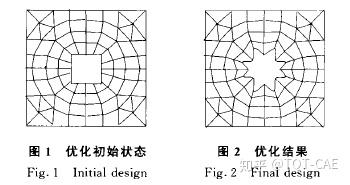
拓扑优化（Topology optimization）：以材料分布为优化对象，通过拓扑优化，可以在均匀分布材料的设计空间中找到最佳的分布方案。

由此可见，拓扑优化相对于尺寸优化和形状优化，具有更多的设计自由度，能够获得更大的设计空间，是结构优化最具发展前景的一个方面。

目前连续体拓扑优化方法主要有均匀化方法 、变密度法、渐进结构优化法（ESO）、水平集方法、可变形孔洞法（Moving Morphable Void，MMV）等。

1）均匀化方法

结构拓扑优化均匀化方法在采用有限元方法对设计区域进行离散化的基础上，将整个设计空间假设成类似“气孔分布”的微结构单元（单胞），单胞在优化开始前分布均匀，大小相同。在拓扑优化过程中，单胞密度分布发生变化，即高应力区域单胞密度变大，低应力区域单胞密度变小。优化过程中形成了一种承重结构，这种结构在高应力区域气孔”密集”，在低应力区域气孔密度较低。当迭代计算全部完成后，再定义一个合理的密度最小值，然后剔除设计空间中单胞密度低于这个最小值的区域，将产生一个材料效应最高的重量优化承重结构。

2）变密度法

变密度方法以连续变量的密度函数形式显式地表达单元相对密度与材料弹性模量之间的对应关系，寻求结构最佳 的传力路线，以实现优化设计区域内的材料分布，具有程序易实现、计算效率快、计算精度高的优势。

3）水平集法

参考知乎@博斌大佬的文章。

目前，连续体拓扑优化的研究已经较为成熟，其中变密度法已经被应用到商用优化软件中，其中最著名的是美国Altair公司Hyperworks系列软件中的OptiStruct和德国Fe-design公司的Tosca（于2013年4月被法国达索收购，已经集成到Abaqus中）等。

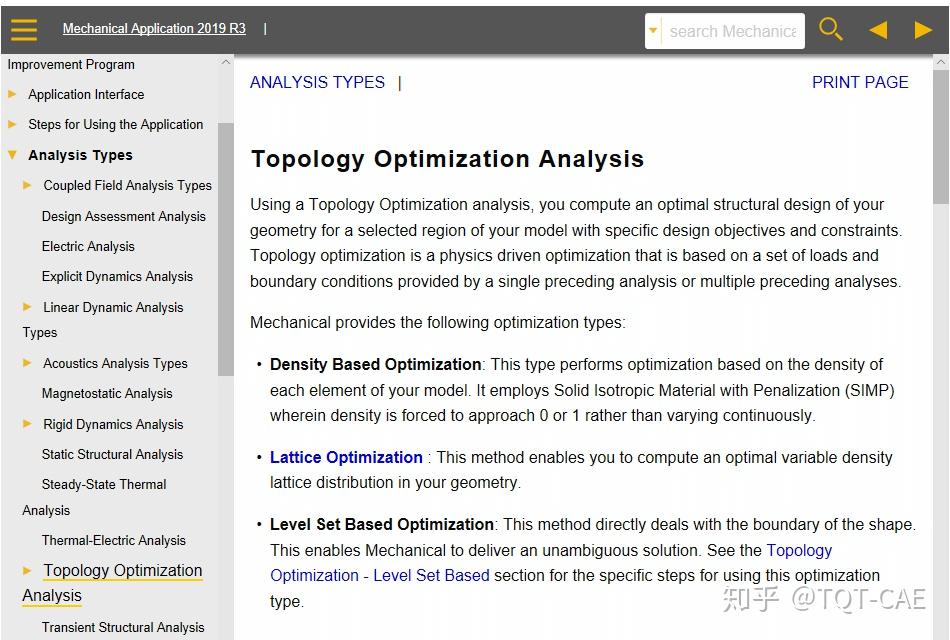
ANSYS中的拓扑优化可选择三种方法：SIMP变密度法，栅格法，水平集法，具有优化准则法和序列凸规划法两种优化算法。

大概五六年前，笔者利用ANSYS12 MAPDL做过零件的拓扑优化，印象中还是有点麻烦。ANSYS MAPDL中是根据单元类型来区分优化区域和排除区域，只对单元类型号为1的区域进行优化。对于不希望优化的区域，用户可以使用单元类型2或更大的单元类型编号来划分网格。

现在的ANSYS Workbench大大降低了拓扑优化的使用难度，可以说，只要会基本的静力分析，就可以完成拓扑优化。

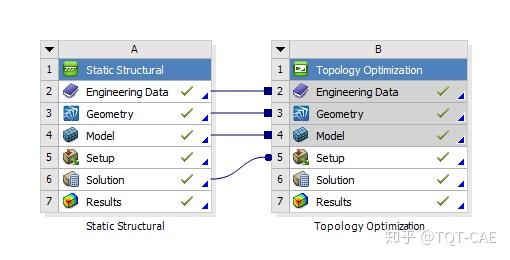
执行完静力分析后，拖入拓扑优化分析，软件作出以下默认设置

• 优化区域为静力分析中所有边界条件（约束和载荷）以外的区域
• 优化目标为最小柔度（最大刚度）
• 响应约束为保留50%质量

不需要任何其他设置即可进行拓扑优化分析，当然也可以根据设计或加工要求，添加其他响应约束（如应力、位移等）和制造约束（如加工尺寸、拔模方向、对称性等）条件。

拓扑优化是设计中具有决定意义的一步，其目的是使设计域内给定量的材料达到最佳的分布形式，为工程师在概念设计阶段提供参考。

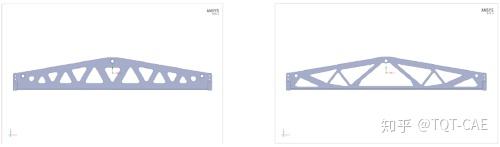
（随手做了个简单案例，非土木桥梁相关专业人士，仅作交流展示，切勿深究）

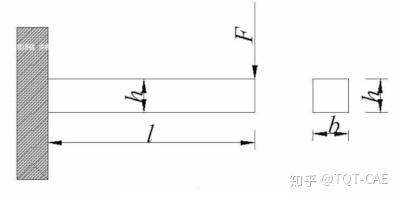
除了在概念设计阶段提供参考，拓扑优化还可用于对原设计方案进行优化。如下图，对我司某吊重梁进行拓扑优化分析，优化后梁的最大应力、变形与原设计基本一致，但重量减轻25%。

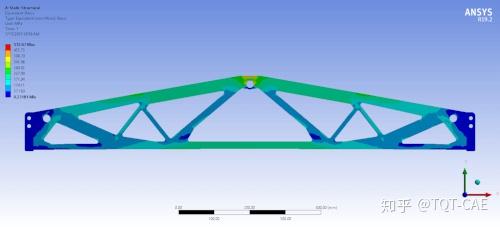
吊重梁优化设计后的应力分布如下图，可以看到，除必须保留的安装孔位外，结构其他区域应力分布均匀。至此，大家是否get到拓扑优化的真谛了呢：材料利用率达到最大化。

说明：上面展示的优化后的吊重梁设计是参考拓扑优化结果，并结合原材料的加工性，进行了重新设计。

1) 支持实体、壳、平面单元类型；

2) 关于网格划分，建议采用细而均匀的网格；

3) 上游分析中的大变形开关设置为关闭；

4) 如果使用了挤压成型约束（Extrusion），优化区域的单元必须为六面体；

5) 如果使用水平集法（level set），要求所有单元必须为四面体；