智能优化算法及其MATLAB实例（第3版）——进化类算法之遗传算法

? ? ? 遗传算法（Genetic Algorithm，GA）是模拟生物在自然环境中的遗传和进化的过程而形成的自适应全局优化搜索算法。它借用了生物遗传学的观点，通过自然选择、遗传和变异等作用机制，实现各个个体适应性的提高。它最早由美国的J. H. Holland教授提出，起源于20世纪60年代对自然和人工自适应系统的研究；70年代，K. A. De Jong基于遗传算法的思想，在计算机上进行了大量的纯数值函数优化计算试验；80年代，遗传算法由D. E. Goldberg在一系列研究工作的基础上归纳总结而成。
? ? ? ?20世纪90年代以后，遗传算法作为一种高效、实用、鲁棒性强的优化技术，发展极为迅速，在机器学习、模式识别、神经网络、控制系统优化及社会科学等不同领域得到广泛应用，引起了许多学者的广泛关注。进入21世纪，以不确定性、非线性、时间不可逆为内涵的复杂性科学成为一个研究热点。遗传算法因能有效地求解NP（Non-deterministic Polynomial）问题以及非线性、多峰函数优化和多目标优化问题，得到了众多学科学者的高度重视，同时这也极大地推动了遗传算法理论研究和实际应用的不断深入与发展。目前，在世界范围内已掀起关于遗传算法的研究与应用热潮。
? ? ? ?遗传算法借鉴了达尔文的进化论和孟德尔的遗传学说，其本质是一种并行、高效、全局搜索的方法，它能在搜索过程中自动获取和积累有关搜索空间的知识，并自适应地控制搜索过程以求得最优解。

（1）遗传算法以决策变量的编码作为运算对象。这种对决策变量的编码处理方式，使得在优化计算过程中可以借鉴生物学中染色体和基因等概念，模仿自然界中生物的遗传和进化等的机理，方便地应用遗传操作算子。特别是对一些只有代码概念而无数值概念或很难有数值概念的优化问题，编码处理方式更显示出了其独特的优越性。
（2）遗传算法直接以目标函数值作为搜索信息。它仅使用由目标函数值变换来的适应度函数值，就可确定进一步的搜索方向和搜索范围，而不需要目标函数的导数值等其他一些辅助信息。实际应用中很多函数无法或很难求导，甚至根本不存在导数，对于这类目标函数的优化和组合优化问题，遗传算法就显示了其高度的优越性，因为它避开了函数求导这个障碍。
（3）遗传算法同时使用多个搜索点的搜索信息。遗传算法对最优解的搜索过程，是从一个由很多个体所组成的初始群体开始的，而不是从单一的个体开始的。对这个群体所进行的选择、交叉、变异等运算，产生出新一代的群体，其中包括了很多群体信息。这些信息可以避免搜索一些不必搜索的点，相当于搜索了更多的点，这是遗传算法所特有的一种隐含并行性。
（4）遗传算法是一种基于概率的搜索技术。遗传算法属于自适应概率搜索技术，其选择、交叉、变异等运算都是以一种概率的方式来进行的，从而增加了其搜索过程的灵活性。虽然这种概率特性也会使群体中产生一些适应度不高的个体，但随着进化过程的进行，新的群体中总会更多地产生出优良的个体。与其他一些算法相比，遗传算法的鲁棒性使得参数对其搜索效果的影响尽可能小。

（5）遗传算法具有自组织、自适应和自学习等特性。当遗传算法利用进化过程获得信息自行组织搜索时，适应度大的个体具有较高的生存概率，并获得更适应环境的基因结构。同时，遗传算法具有可扩展性，易于同别的算法相结合，生成综合双方优势的混合算法。

? ? ? ?标准遗传算法的主要本质特征，在于群体搜索策略和简单的遗传算子，这使得遗传算法获得了强大的全局最优解搜索能力、问题域的独立性、信息处理的并行性、应用的鲁棒性和操作的简明性，从而成为一种具有良好适应性和可规模化的求解方法。但大量的实践和研究表明，标准遗传算法存在局部搜索能力差和“早熟”等缺陷，不能保证算法收敛。

? ? ? 在现有的许多文献中出现了针对标准遗传算法的各种改进算法，并取得了一定的成效。它们主要集中在对遗传算法的性能有重大影响的6个方面：编码机制、选择策略、交叉算子、变异算子、特殊算子和参数设计（包括群体规模、交叉概率、变异概率）等。

? ? ? ?此外，遗传算法与差分进化算法、免疫算法、蚁群算法、粒子群算法、模拟退火算法、禁忌搜索算法和量子计算等结合起来所构成的各种混合遗传算法，可以综合遗传算法和其他算法的优点，提高运行效率和求解质量。

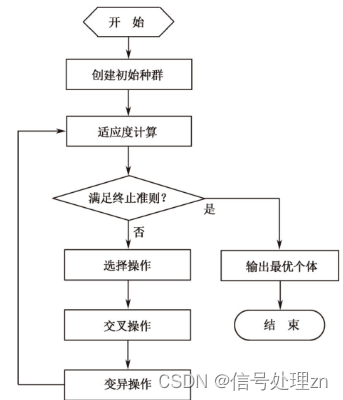
遗传算法的运算流程如下图所示，具体步骤如下：

(1）初始化。设置进化代数计数器g=0，设置最大进化代数G，随机生成NP个个体作为初始群体P(0)。
(2)个体评价。计算群体P( t)中各个个体的适应度。
(3）选择运算。将选择算子作用于群体，根据个体的适应度，按照一定的规则或方法，选择一些优良个体遗传到下一代群体。
(4)交叉运算。将交叉算子作用于群体，对选中的成对个体，以某一概率交换它们之间的部分染色体，产生新的个体。
(5）变异运算。将变异算子作用于群体，对选中的个体，以某一概率改变某一个或某一些基因值为其他的等位基因。群体P( t）经过选择、交叉和变异运算之后得到下一代群体P( t+1)。计算其适应度值，并根据适应度值进行排序，准备进行下一次遗传操作。
(6)终止条件判断:若g≤G，则g= g+1，转到步骤（2)﹔若g>G，则此进化过程中所得到的具有最大适应度的个体作为最优解输出，终止计算。

用标准遗传算法求函数f ( x ) =x+10sin ( 5x )+7cos (4x）的最大值，其中x的取值范围为[0，10]。

解：仿真过程如下：
（1）初始化种群数目为NP=2050，染色体二进制编码长度为L=20，最大进化代数为G=1000，交叉概率为0.8，变异概率为0.1。
（2）产生初始种群，将二进制编码转换为十进制，计算个体适应度值，并进行归一化；采用基于轮盘赌的选择操作、基于概率的交叉和变异操作，产生新的种群，并把历代的最优个体保存在产生新种群中，进行下一次遗传操作。
（3）判断是否满足终止条件：若满足，则结束搜索过程，输出优化值；若不满足，则继续进行迭代优化。

优化结束后，其实适应度

MATLAB代码如下：

?计算函数的最小值，其中个体x的维数r=10。这是一个简单的平方和函数，只有一个极小点(0，0，…，0)，理论最小值f (0，0，…，0）=0。

?MATLAB代码如下：

运行结果：

Bestf =

? ?-0.0017
? ? 0.0007
? ?-0.0049
? ? 0.0016
? ? 0.0019
? ?-0.0025
? ?-0.0122
? ?-0.0028
? ? 0.0224
? ?-0.0082

ans =

? ?7.6289e-04

旅行商问题（TSP问题）。假设有一个旅行商人要拜访全国31个省会城市，他需要选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。对路径选择的要求是：所选路径的路程为所有路径之中的最小值。
解：仿真过程如下：
（1）初始化种群数目为NP=200，染色体基因维数为N=31，最大进化代数为G=1000
（2）产生初始种群，计算个体适应度值，即路径长度；采用基于概率的方式选择进行操作的个体；对选中的成对个体，随机交叉所选中的成对城市坐标，以确保交叉后路径每个城市只到访一次；对选中的单个个体，随机交换其一对城市坐标作为变异操作，产生新的种群，进行下一次遗传操作。
（3）判断是否满足终止条件：若满足，则结束搜索过程，输出优化值；若不满足，则继续进行迭代优化。

MATLAB代码如下：

优化后的路径，其适应度进化曲线如图所示。

有N件物品和一个容量为V背包。第件物品的体积是c（i），价值是w（i）。求解将哪些物品放入背包可使物品的体积总和不超过背包的容量，且价值总和最大。假设物品数量为10，背包的容量为300。每物积为[95，75，23，73，50，22，6，57，89，98]，价值为[89，59，19，43，100，72，44，16，7，64]。
解：仿真过程如下：
（1）初始化种群数目为NP=50，染色体基因维数为L=10，最大进化代数为G=100
2）产生二进制初始种群，其中1表示选择该物品，0表示不选择该物品。取适应度值为选择物品的价值总和，计算个体适应度值，当物品体积总和大于背包容量时，对适应度值进行惩罚计算。
（3）对适应度进行归一化，采用基于轮盘赌的选择操作、基于概率的交叉和变异操作，产生新的种群，并把历代的最优个体保留在新种群中，进行下一步遗传操作。
（4）判断是否满足终止条件：若满足，则结束搜索过程，输出优化值；若不满足，则继续进行迭代优化。
优化结果为[1010111001]，1表示选择相应物品，0表示不选择相应物品，价值总和为388，其适应度进化曲线如所示。
MATLAB代码如下：